Standard Addition Method

In analytical chemistry, a calibration equation is generally used to determine the unknown concentration of an analyte. The equation is developed by evaluating the sensor’s response to a series of standards with known concentrations of the same analyte. The calibration equation method normally requires an identical matrix for both sample and standards, which won’t interfere with the analyte signal. Whereas within complex or unknown sample matrices such as biological fluids, liquids with heavy metals, and soils, etc., the analyte signal can interfere with the components other than the analyte itself, a.k.a. matrix effect. Thus, the direct comparison between the sample and standards becomes invalid.

For better accuracy in the analysis of such samples, the standard addition method can be adopted to reduce the discrepancies between samples and standards. The standard addition method, a.k.a. “spiking,” can also account for similar matrix effects in the calibration equation by adding known amounts of analytes to the samples. In doing so, a change in the sensor response between a sample and a spiked sample is assumed to be due only to the change in the analyte concentration.

Standard Addition Procedure

Equal volumes of a series of test solutions (V_T) are prepared, which also contain equal volumes of the sample (VX) with unknown concentration (CX). In addition, increasing volumes of analyte standards with a known concentration (C_S) are also spiked into all solutions except one, which comprises of sample and solvent only. A calibration curve of the sensor response to these solutions can be plotted by placing the spiked volume of the analyte standards (V_S) on the x-axis and the corresponding sensor response (S) on the y-axis, as shown in the graph below. 

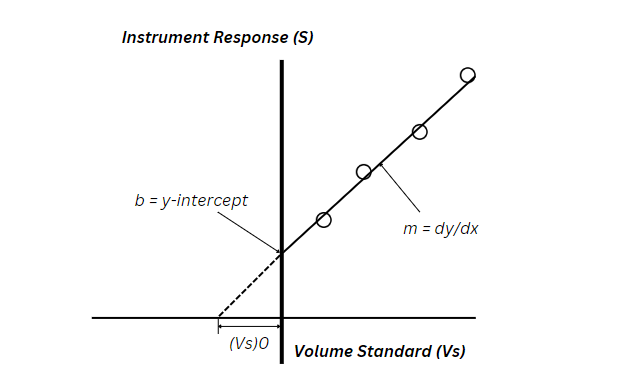
Linear regression is performed, and the slope (m) and y-intercept (b) of the calibration curve
are used to calculate the analyte concentration in the sample. From the linear regression:

   

In Equation 1, S represents the instrument response (signal), while V_S is the volume of standard.

Conceptually, if the curve starts where the instrument response is zero. Then, the volume of standard [(V_S)0] from that point to the point of the first solution on the curve (x = 0) will contain the same amount of analyte as the sample. So:

   

In Equation 2, V_x is the volume of the sample aliquot, cx is the concentration of the sample, and c_s is the concentration of the standard. Combining Equation 1 and Equation 2, and solving for c_x results in:

   

Then one can calculate the concentration of analyte in the sample from the slope and intercept of the standard addition calibration curve.